2024.7.15 训练记录

P3034 USACO - Cow Photography

P3034

看到题，第一眼考虑将五次拍照的序列经过一些方法组合得到原序列，思考后发现不好做；我们考虑不变量，每次有一个元素随意移动到新的位置，对于序列元素的绝对位置其实不怎么好刻画，因为可能会产生整体偏移；但仔细一想，这一操作对序列元素的 相对位置 影响不大，因此我们考虑序列元素的相对位置关系

思路已经有了，问题来了，怎么确定要考察的两个元素不是在该次移动的元素呢？题目其实给了一个很重要的条件 —— 一个元素最多只会移动一次，因此我们从整体考虑，对于序列中的两元素 \(a_i, a_j (i<j)\)，会对其相对位置造成影响的移动 最多只会出现 \(2\) 次，即将 \(a_j\) 挪到 \(a_i\) 前或将 \(a_i\) 挪到 \(a_j\) 后，题目刚好给了 \(5\) 次拍照结果，因此我们考察元素 \(a_i, a_j\)，如果有 \(3\) 次拍照结果中都有 \(i<j\)，那么在原序列中就有 \(i<j\)

由此知道了原序列中任意两元素的相对位置关系，现在我们希望求出原序列，正好发现 \(sort\) 的 \(cmp\) 函数可以完美切合这个问题，因此直接任取一次拍照结果 \(sort\) 一遍，排序结果就是原序列

实现细节上，我们要记录在第 \(i(1\le i \le 5)\) 次拍照中元素 \(a_i (0 \le a_i \le 1000000000)\) 的位置，值域很大，因此使用 \(map\) 记录，开 \(O2\) 即可水过；事实上由于本题中没有查询，使用 \(umap\) 会更快，实测不开 \(O2\) 最慢点约 \(700ms\)，可过

时间复杂度 \(O(nlogn)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e4+5;

int N;
int A[6][MAXN];
int ans[MAXN];

unordered_map <int, unordered_map <int, int> > pos;

bool cmp(int a, int b){
    int cnt=0;
    for (int i=1; i<=5; i++){
        if (pos[i][a] < pos[i][b]){
            cnt++;
        }
    }
    if (cnt >= 3){
        return true;
    }
    return false;
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=5; i++){
        for (int j=1; j<=N; j++){
            scanf("%d", &A[i][j]);
            pos[i][A[i][j]] = j;
        }
    }
    for (int i=1; i<=N; i++){
        ans[i] = A[1][i];
    }

    sort(ans+1, ans+N+1, cmp);

    for (int i=1; i<=N; i++){
        printf("%d\n", ans[i]);
    }
    return 0;
}

P4188 USACO - Lifeguards S

P4188

我们考虑先求出所有区间覆盖的 时间点，再减去单个区间中与其他区间 不重叠 时间点的数量最小值；注意这里是时间点，所以如果给定区间 \(l, r (l \le r)\)，实际上覆盖的时间点有 \(r-l\) 个而非 \(r-l+1\) 个

先考虑如何求出所有区间覆盖的时间点。首先必不可少的肯定是先给区间按照左端点 \(sort\) 一遍；接下来使用类似双指针的思想，考虑新加入线段 \(line[i]\)，参照下图，我们定义 \(borderr\) 表示新加入线段前 己经加入的线段能够覆盖的最大时间点，\(line[i].l\) 表示目前区间的左端时间点，\(line[i].r\) 表示目前区间的右端时间点

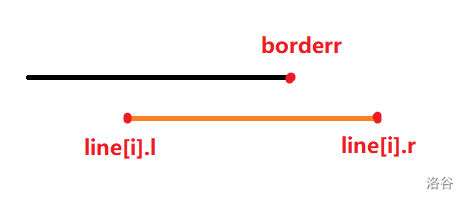
容易发现，如果 \(line[i].r \le borderr\)，那么当前线段没有真正产生贡献，跳过即可；当 \(line[i].r > borderr\) 时，我们希望求出当前线段 左侧不与先前加入线段重叠的最大时间点，设为 \(recentl\)，这样该线段的贡献即为 \(line[i].r - recentl\)，如下图为两种不同情况，易得 \(recentl = max(borderr, line[i].l)\)

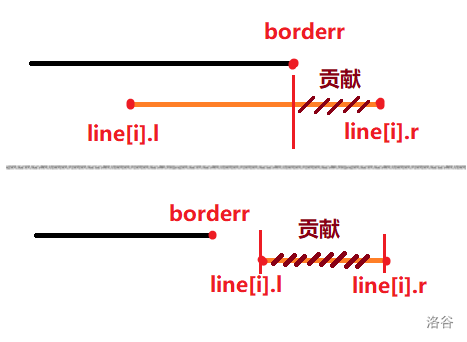
因此枚举每个区间统计即可，别忘了每次统计后还要更新 \(borderr\)，直接令 \(borderr = line[i].r\) 即可，这样我们就解决了总贡献

接下来考虑如何求出单个区间的贡献。设当前区间为 \(line[i]\)，首先仍然要特判 \(line[i].r \le borderr\)，这说明有区间被完全包含，此时 \(break\) 后直接输出总贡献即可；最坏情况下，单个区间 \(line[i]\) 可能会与之前的区间产生重叠，也会与后一个区间 \(line[i+1]\) 产生重叠，我们考虑 \(line[i].l\) 与 \(borderr\)、\(line[i].r\) 与 \(line[i+1].l\) 的关系，左端点处最大无重叠时间点即为 \(max(line[i].l, borderr)\)，右端点最大无重叠时间点即为 \(min(line[i].r, line[i+1].l)\)，可以结合下图理解

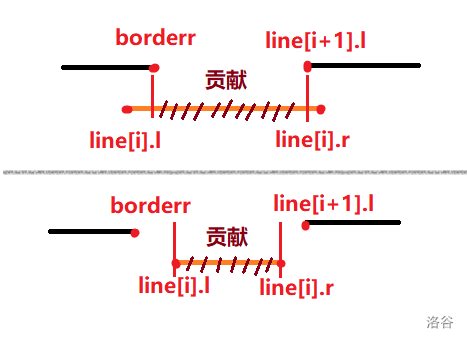
因此我们统计处最小的单个区间贡献，最终用总贡献减去即可得到最终答案；实现时注意该贡献可能为 负数，此时可以特判为 \(0\) 并直接 \(break\)；同时，和统计总贡献时相同，也别忘了更新 \(borderr\) 即 \(borderr = line[i].r\)

时间复杂度 \(O(nlogn)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;

int N;
long long sum, mcover=1e9;

struct Line{
    int l;
    int r;
}line[MAXN];

bool cmp(Line a, Line b){
    if (a.l == b.l){
        return a.r < b.r;
    }
    return a.l < b.l;
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=N; i++){
        scanf("%d%d", &line[i].l, &line[i].r);
    }
    sort(line+1, line+N+1, cmp);

    int borderr = 0;
    for (int i=1; i<=N; i++){
        if (line[i].r > borderr){
            int recentl = max(line[i].l, borderr);
            sum += line[i].r-recentl;
            borderr = line[i].r;
        }   
    }

    borderr = 0;
    line[N+1].l = line[N].r;
    for (int i=1; i<=N; i++){
        if (line[i].r <= borderr){
            mcover = 0;
        }
        else{
            long long cover = min(line[i+1].l, line[i].r)-max(line[i].l, borderr);
            mcover = min(mcover, cover);
            borderr = line[i].r;
        }

        if (mcover <= 0){
            mcover = 0;
            break;
        }   
    }

    printf("%lld", sum-mcover);
    return 0;
}

P4181 USACO - Rental Service S

P4181

每个奶牛有两种分配方式，一种是将奶牛租出去，一种是卖出该奶牛生产的奶；首先注意到租奶牛这一方式对具体租哪一只奶牛没有限制，因此易得贪心，即 优先租产奶量小的奶牛，同时 优先租给价格最高的农场主；同理，卖奶时也 优先卖给价格最高的商店

因此，我们将商店按照价格 从大到小排序、将租奶牛的农场主按照租用价格 从大到小排序；我们注意到将所有奶牛排序后，必然有从头连续一部分选择租出去，剩下一部分选择卖出去，因此考虑 枚举断点 \(i\) ，钦定将第 \(1\) 到第 \(i\) 头奶牛的奶卖出去，第 \(i+1\) 到第 \(N\) 头奶牛租出去；所以，我们也要对奶牛按照产奶量 从大到小排序

这样，我们将总贡献分为两部分，一部分来自租出奶牛；这一部分很好维护，直接上 前缀和 即可，对排序后的 \(r[i]\) 数组，定义 \(sum[i]\) 为其前缀和数组，表示租出 \(i\) 头牛能得到的钱

对于卖奶牛奶的部分，虽然卖出奶的总和也可以用前缀和维护，但如果每次都从第 \(i\) 个商店向后循环处理是否能卖出奶会超时；由于我们知道相邻两次卖奶总和的 增量 (设当前奶牛为 \(i\)，这个增量实际上就是 \(c[i]\))，因此可以 直接考虑其对答案的影响，记录下上一次卖完后所得所有的钱 \(sell\)，当前卖到的商店位置 \(cnt\)，直接进行处理即可；这里有个技巧，我们可以单独开一个变量记录当前商店中已有的牛奶 \(storemilk\)，这样省去了直接改动商店原本信息的麻烦

具体的，设当前要卖出的牛奶 (增量) 为 \(milk=c[i]\)，第 \(i\) 个的商店的容量为 \(store[i].q\) (实际剩余容量为 \(store[i].q-storemilk\)) 、价格为 \(store[i].p\)，分情况讨论；

1. 当商店剩余容量不足 \(milk\) 时
   • 用 \(store[i].q-storemilk\) 更新 \(sell\)
2. 更新当前要卖出的牛奶数量 \(milk\)
3. 收回 \(storemilk\)，将其设为 \(0\)
4. 别忘了进行 \(cnt+1\)
5. 当商店剩余容量够 \(milk\) 时
6. 用 \(milk\) 更新 \(sell\) (特别注意！这里不是 \(storemilk+milk\))
7. 更新 \(storemilk\) (因为这里 \(store[i].q\) 的变化实际上直接体现在了 \(storemilk\) 的变化上)
8. 跳出循环即可，因为已经卖光了

最终统计出当前的总价值，加上租出的价值，与最终答案 \(ans\) 比较，这里如果 当前总价值 $ \le ans$，其实 可以直接 \(break\) ，因为容易证明价值变化分界点唯一

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;

int N, M, R;
int c[MAXN], r[MAXN];
long long sumr[MAXN];
long long ans = 0;

struct Store{
    int p;
    int q;
}store[MAXN];

bool cmp(int a, int b){
    return a>b;
}
bool cmp_store(Store a, Store b){
    if (a.p == b.p){
        return a.q > b.q;
    }
    return a.p > b.p;
}

int main(){
    scanf("%d%d%d", &N, &M, &R);

    for (int i=1; i<=N; i++){
        scanf("%d", &c[i]);
    }
    sort(c+1, c+N+1, cmp);
    for (int i=1; i<=M; i++){
        scanf("%d%d", &store[i].q, &store[i].p);
    }
    sort(store+1, store+M+1, cmp_store);
    for (int i=1; i<=R; i++){
        scanf("%d", &r[i]);
    }
    sort(r+1, r+R+1, cmp);

    for (int i=1; i<=R; i++){
        sumr[i] = sumr[i-1]+r[i];   
    }

    long long storemilk=0, cnt=1;
    long long sell=0, rent=0;

    for (int i=0; i<=N; i++){
        long long milk = c[i];
        while (cnt<=M){
            if (milk+storemilk >= store[cnt].q){
                milk = milk+storemilk-store[cnt].q;
                sell += 1ll*(store[cnt].q-storemilk)*store[cnt].p;
                storemilk = 0;
                cnt++;
            }   
            else{
                sell += 1ll*milk*store[cnt].p;
                storemilk = milk+storemilk;
                break;
            }
        }   
        rent = sumr[min(N-i, R)];
        if (rent+sell > ans){
            ans = rent+sell;
        }
        else{
            break;
        }
    }

    printf("%lld", ans);
    return 0;
}

P4265 - USACO Snow Boots S

P4265

考虑 \(DP\)；设 \(dp[i]\) 表示到第 \(i\) 格所穿的靴子编号 (也就是丢弃了 \(dp[i]-1\) 双靴子)，考虑转移，显然到第 \(i\) 格只能由前面的格子转移而来，因此枚举 \(j (1 \le j < i)\)；因为我们要么直接穿着在第 \(j\) 格的靴子走到第 \(i\) 格，要么在第 \(j\) 格脱下一些靴子再走到第 \(i\) 格，所以再枚举 \(k (dp[j] \le k \le B)\)，表示到达第 \(i\) 格时所穿的靴子

我们想从第 \(j\) 格穿着第 \(k\) 个靴子走到第 \(i\) 格，需要： - 第 \(k\) 个靴子能够走在第 \(j\) 格的雪上 - 第 \(k\) 个靴子能够走在第 \(i\) 格的雪上 - 第 \(k\) 个靴子能走的距离至少是 \(i\) 到 \(j\) 的距离

转移方程很简单，就是 \(dp[i] = min(dp[i], k)\)，答案即为 \(dp[N]-1\)，注意不要忘记 \(-1\)

初始情况为 \(dp[1] = 0\)，因为一开始不穿靴子，另外由于需要求最小值，别忘了在最开始 \(memset\) 一下

时间复杂度 \(O(N^2B)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 305;

int N, B;
int h[MAXN], s[MAXN], d[MAXN];
int dp[MAXN];

int main(){
    scanf("%d%d", &N, &B);

    for (int i=1; i<=N; i++){
        scanf("%d", &h[i]);
    }
    for (int i=1; i<=B; i++){
        scanf("%d%d", &s[i], &d[i]);
    }

    memset(dp, 0x3f, sizeof(dp));
    dp[1] = 0;
    for (int i=2; i<=N; i++){
        for (int j=1; j<i; j++){
            for (int k=dp[j]; k<=B; k++){
                if (s[k] >= h[i] && s[k] >= h[j] && d[k]>=i-j){
                    dp[i] = min(dp[i], k);
                }
            }   
        }
    }

    printf("%d", dp[N]-1);
    return 0;
}

P4264 USACO - Teleportation S

P4264

不会。咕咕咕。

评论