跳转至

2024.7.16 训练记录

BNDSOJ USACO - Grazing Patterns

Grazing Patterns

看到题，首先考虑暴力 \(bfs\)；我们将两个起点都存入队列中，当两点移动到同一位置且走过步数之和为 \(25-K\) 时更新答案；实际上，实现起来发现这种做法较为烦琐，因此我们先考虑对题意进行一些简化

实际上，题面中两牛各走出了一条有向路径，且这两条有向路径 终点相同，且 长度相同；考虑对路径进行转化，由于两路径终点相同，我们可以将米尔德里德走出的路径 反向 一下，这样米尔德里德走出的路径起点就为贝茜走出的路径的终点，米尔德里德走出的路径的终点即为 \((5, 5)\)；这样两牛的路径就被 合成为一条从 \((1, 1)\) 到 \((5, 5)\) 的路径，又因为合称前两路径长度相同，原相交点实际上也是可以唯一确定的；

因此，我们实际要求的就是从 \((1, 1)\) 走到 \((5, 5)\) 且恰好覆盖了整个地图的路径数量，\(dfs\) 即可

代码

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
int K, ans=0;
int mp[6][6];
int mv[4][2] = {1, 0, -1, 0, 0, 1, 0, -1};
bool vis[6][6];

void dfs(int x, int y, int step){
    if (x == 5 && y == 5 && step == 25-K){
        ans++;
        return;
    }

    for (int i=0; i<4; i++){
        int nx = x+mv[i][0];
        int ny = y+mv[i][1];

        if (nx<1 || ny<1 || nx>5 || ny>5){
            continue;
        }
        if (mp[nx][ny] == -1 || vis[nx][ny]){
            continue;
        }

        vis[nx][ny] = true;
        dfs(nx, ny, step+1);
        vis[nx][ny] = false;
    }   
}

int main(){
    scanf("%d", &K);

    for (int i=1; i<=K; i++){
        int x, y;
        scanf("%d%d", &x, &y);
        mp[x][y] = -1;
    }

    vis[1][1] = true;
    dfs(1, 1, 1);
    printf("%d", ans);
    return 0;
}

P1884 USACO - Overplanting S

P1884

这道题实际上是扫描线板子，可是我不会呀

首先考虑暴力。有一个很显然的做法，对于一个左上角、右下角坐标分别为 \((lx, ly), (rx, ry)\) 的矩形，枚举 \(x(lx < x \le rx)\) 与 \(y(ry \le y < rx)\)，开一个 \(vis\) 数组记录这样的点 \((x, y)\) 是否统计过，如果没有统计过就更新答案并更新 \(vis\) 数组；这种做法很显然会超时

我们注意到暴力做法实际上是通过枚举矩形内每个点来保证不会重复计算面积，这种做法比较直观但很低效；其实问题的关键就在于 如何保证不会重复计算面积，考虑新加入矩形 \((lx, ly), (rx, ry)\)，对于之前的任一矩形 \((lx', ly'), (rx', ry')\)，新加入的矩形可能会与该矩形产生重叠，那么我们可以考虑把原来的矩形 分割为一些与新矩形不重叠的矩形，这样就解决了重复计算的问题

实现细节上，我们如果直接考虑新矩形整体与原矩形整体的位置关系，会发现有很多情况需要讨论，比较麻烦；其实我们可以直接考虑新矩形 各边 与原矩形对应各边的关系，即 按边分割；举个例子，如果新矩形的下边比原矩形的下边高，说明原矩形底部需要分割出一块小矩形；可以参照下图理解，当新矩形被原矩形完全包含时，我们实际上将原矩形分割成了四块

分割图片

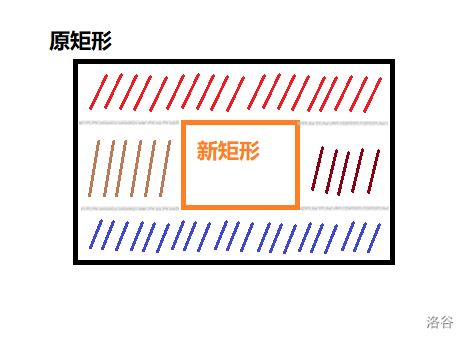
代码

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e6+5;

int N, front=0, rear=0;
long long ans;

struct Rec{
    int lx;
    int ly;
    int rx;
    int ry;
}rec[MAXN];

void Cut(Rec rec1, Rec rec2){
    // cout << "use!" << endl;
    if (rec2.ly <= rec1.ry || rec2.ry >= rec1.ly || rec2.lx >= rec1.rx || rec2.rx <= rec1.lx){
        rec[rear].lx = rec1.lx;
        rec[rear].ly = rec1.ly;
        rec[rear].rx = rec1.rx;
        rec[rear].ry = rec1.ry;
        rear++;
        return;
    }   
    if (rec2.ly < rec1.ly){
        rec[rear].lx = rec1.lx;
        rec[rear].ly = rec1.ly;
        rec[rear].rx = rec1.rx;
        rec[rear].ry = rec2.ly;
        rear++;
    }
    if (rec2.ry > rec1.ry){
        rec[rear].lx = rec1.lx;
        rec[rear].ly = rec2.ry;
        rec[rear].rx = rec1.rx;
        rec[rear].ry = rec1.ry;
        rear++;
    }
    if (rec2.lx > rec1.lx){
        rec[rear].lx = rec1.lx;
        rec[rear].ly = min(rec1.ly, rec2.ly);
        rec[rear].rx = rec2.lx;
        rec[rear].ry = max(rec1.ry, rec2.ry);
        rear++;
    }
    if (rec2.rx < rec1.rx){
        rec[rear].lx = rec2.rx;
        rec[rear].ly = min(rec1.ly, rec2.ly);
        rec[rear].rx = rec1.rx;
        rec[rear].ry = max(rec1.ry, rec2.ry);
        rear++;
    }
    return;
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=N; i++){
        scanf("%d%d%d%d", &rec[rear].lx, &rec[rear].ly, &rec[rear].rx, &rec[rear].ry);
        int recentrear = rear;
        rear++;

        for (int j=front; j<recentrear; j++){
            Cut(rec[j], rec[recentrear]);
            front++;    
        }
    }

    for (int i=front; i<=rear; i++){
        // cout << "id " << i << ": " << rec[i].lx << " " << rec[i].ly << " " << rec[i].rx << " " << rec[i].ry << endl;
        ans += 1ll*(rec[i].rx-rec[i].lx)*(rec[i].ly-rec[i].ry); 
    }

    printf("%lld", ans);
    return 0;
}

P4087 USACO - Milk Measurement S

P4087

记产量最大的牛的个数 \(cnt1\)，我们发现，如果照片需要被调整，要么是 \(cnt1\) 发生变化，要么就是具体的牛有变化；按照这个思路，我们先具体分析一下如果照片需要被改变，可能需要满足什么条件

具体的，我们考虑分情况讨论：记 \(recentmilk\) 为 测量前 的最大产量，\(recentcnt\) 为测量前最大产量的个数，\(maxmilk\) 为 测量后 的最大产量，\(maxcnt\) 为测量后最大产量的个数

  1. 测量后最大产量不变 (\(recentmilk = maxmilk\))

1.1 测量后 最大个数发生变化，即此时 \(recentcnt \ne maxcnt\)，那么显然照片要发生变化

1.2 测量后最大个数不变化，即此时 \(recentcnt = maxcnt\) ，我们反证：如果照片还会发生改动，那么只能是测量后具体的牛发生了变化，即有一头牛上来有一头牛下去，但一次测量只能改变一头牛，因此这种情况不成立

  1. 测量后最大产量变化 (\(recentmilk \ne maxmilk\))

2.1 测量后 最大个数发生变化，显然照片也要发生变化

2.2 如果最大个数不变：

2.2.1 一头测量前产量最大的牛经过测量后产量发生变化。再分产量变大或变小两种情况讨论

2.2.1.1 其产量变大。此时最大个数会发生变化 (变成 \(1\))，又由于最大个数不变，那么原本的最大个数就是 \(1\)，这样对照片不会产生影响

2.2.1.2 其产量变小。如果其变小后仍然产量最大，此时又由于最大个数不变，那就说明原来的最大个数是 \(1\)，现在还是 \(1\)，此时对照片不产生影响。另一种情况，如果其变小后不再是产量最大的牛，说明变小后有另一些牛的产量比它大了，那么照片需要变化

2.2.2 一头测量前产量不是最大的牛经过测量后产量变为最大。此时最大个数变为 \(1\)，那么原本的最大个数也为 \(1\)，又因为此时具体的牛发生变化，所以照片需要变化

我们对上面的讨论进行总结，如果照片会发生变化，可能有如下情况

  1. 测量后 最大个数发生变化，即 \(recentcnt \ne maxcnt\)
  2. 测量后最大产量发生变化，而该次变化的牛为测量前产量最大的牛，其产量变小，变化后不再是产量最大的牛；又因为如果其产量变大，一定是产量最大的牛，所以该条也可以表述为测量后最大产量发生变化，且该次变化的牛为测量其产量最大的牛，其变化后不再是产量最大的牛；进一步的，如果该次变化的牛不是测量前产量最大的牛，原本产量最大的牛最终也不会是产量最大的牛；因此可以进一步表述为 测量后最大产量发生变化，且变化后原本最大产量的牛不再是现在最大产量的牛
  3. 测量后最大产量发生变化，且为测量前产量非最大的牛发生变化

现在我们就解决了何时照片会变化的问题，全程只需要维护 \(recentmilk, maxmilk, recentcnt, maxcnt\) 与支持给定奶牛查询奶牛当前产奶量、给定奶量查询当前产奶量为该奶量的奶牛有多少个的数据结构；容易发现这些数据结构只需要支持单点改单点查，因此我们没必要开线段树，只开 \(map\) 即可

我们枚举每一次测量，按题意对两个 \(map\) 进行维护，维护前进行 \(recentmilk = maxmilk, recentcnt = maxcnt\) 存储上一次的信息，维护后更新 \(maxmilk\) 与 \(maxcnt\)，再记录本次更改是否更改的是最大牛，更改后原本最大牛是否还是最大牛，按照总结出的条件进行维护即可

代码

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5, INF = 2e9;

int N, G, ans;

struct Measure{
    int day;
    int id;
    long long c;
}m[MAXN];

bool cmp(Measure a, Measure b){
    return a.day < b.day;
}

map <int, long long> milk;
map <int, int> cnt;

int main(){
    scanf("%d%d", &N, &G);

    for (int i=1; i<=N; i++){
        scanf("%d%d%lld", &m[i].day, &m[i].id, &m[i].c);
    }
    sort(m+1, m+N+1, cmp);

    long long maxmilk=0, recentmilk=0;
    int maxcnt=INF, recentcnt=0;
    bool flagbefore = false, flagafter = false;
    cnt[0] = INF;

    for (int i=1; i<=N; i++){
        if (milk[m[i].id] == maxmilk){
            flagbefore = true;
        }
        else{
            flagbefore = false;
        }
        cnt[milk[m[i].id]]--;
        if (cnt[milk[m[i].id]] == 0){
            cnt.erase(milk[m[i].id]);
        }
        milk[m[i].id]+=m[i].c;
        cnt[milk[m[i].id]]++;

        recentmilk = maxmilk;
        recentcnt = maxcnt;
        auto it = cnt.end();
        it--;
        maxmilk = (*it).first;
        maxcnt = (*it).second;
        if (milk[m[i].id] == maxmilk){
            flagafter = true;
        }
        else{
            flagafter = false;
        }

        if (maxcnt != recentcnt){
            ans++;
        }
        else if ((flagbefore == false || flagafter == false) && (maxmilk != recentmilk)){
            ans++;
        }
    }
    printf("%d", ans);
    return 0;
}

P4089 USACO - The Bovine Shuffle

P4089

我们观察到，如果 \(i, a[i], a[a[i]], ...\) 形成一个环，则在这个环里的奶牛只会在这个环里按顺序来回跳；又因为初始时这个环上的每个点都有奶牛，则 任意时刻这个环上也都有奶牛。

因此，我们将每个 \(i\) 对 \(a[i]\) 连边，拓扑排序 判环即可，最终拓扑排序删不掉的点的个数就是答案

代码

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;

int N, ans;
int a[MAXN], in[MAXN];

vector <int> G[MAXN];

void TopoSort(){
    queue <int> S;

    for (int i=1; i<=N; i++){
        if (in[i] == 0){
            S.push(i);
        }   
    }

    while (!S.empty()){
        int recent = S.front();
        S.pop();
        ans++;

        for (int i=0; i<G[recent].size(); i++){
            in[G[recent][i]]--;
            if (in[G[recent][i]] == 0){
                S.push(G[recent][i]);
            }
        }
    }
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=N; i++){
        scanf("%d", &a[i]);
        G[i].push_back(a[i]);
        in[a[i]]++;
    }

    TopoSort();
    printf("%d", N-ans);
    return 0;
}

P4378 Out Of Sorts S

P4378

本质上，一次循环会消掉每个位置上的一个逆序对；因此，逆序对最多的一个位置的逆序对个数 \(+1\) 即为答案；

我们感性理解，将数列从小到大排序，认为每个元素前移的距离反映了其原位置上逆序对的数量；但是这么做有问题，每个元素前移的距离并不能真正代表其原位置上逆序对数量，举个例子，设原数列为 \(3, 2, 1\)，排序后为 \(1, 2, 3\)，元素 \(2\) 前移的距离为 \(0\)，但实际上其原位置上有一个逆序对 \((3, 2)\)；

问题出在哪呢？我们发现，\(2\) 前面有一个 \(1\)，顶掉了一个前移的距离，这说明若一个元素 \(a_i\) 后有比它的值还小的元素 \(a_j (a_j < a_i)\)，排序后 \(a_j\) 会变到 \(a_i\) 前面影响原 \(a_i\) 位置上的逆序对个数统计；但又由于我们 只关注逆序对数最大的位置，由于 \(a_i > a_j\)，\(a_i\) 及以前所有大于等于它的元素都会大于 \(a_j\)，所以 \(a_j\) 位置上的逆序对个数严格大于 \(a_i\)，这样我们只关注 \(a_j\) 即可，\(a_i\) 位置上的逆序对数量统计差异对答案 没有影响

因此，我们将原序列排序，统计元素的 最大移动距离，最后 \(+1\) 即可 (为什么 \(+1\)? 因为最终冒泡排序完成后还要再扫一遍确定已经不需要再来一轮)

代码

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;

int N, ans;

struct Node{
    int val;
    int pos;
}num[MAXN];

bool cmp(Node a, Node b){
    if (a.val == b.val){
        return a.pos < b.pos;
    }
    return a.val < b.val;
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=N; i++){
        scanf("%d", &num[i].val);
        num[i].pos = i;
    }
    sort(num+1, num+N+1, cmp);

    for (int i=1; i<=N; i++){
        ans = max(ans, num[i].pos-i);
    }
    printf("%d", ans+1);
    return 0;
}

P4380 USACO - Multiplayer Moo S

P4380

第一问简单 \(dfs\) 即可，关键在于第二问

首先有一个思路，直接枚举每个相邻且颜色不同的方格，以这两个颜色为基准颜色，暴力进行 \(dfs\) 统计答案；这样肯定可以写，但比较麻烦，这里有一个更好的思路

在进行第一遍 \(dfs\) 时，我们实际上已经能够得出每个连通块的基本信息 (如大小，颜色)，没必要在第二遍再 \(dfs\) 一次；因此，第一遍时我们记录下每个连通块的大小 \(siz\) 与颜色 \(col\)，开结构体存储，同时开二维数组 \(belong[i][j]\) 表示 \((i, j)\) 格属于哪个连通块；求第二问时，我们仍然枚举每个方格，但这次是为了在相邻的连通块间 连边

连好后，我们得到了一个无向连通图，希望求出相邻的、颜色为两个颜色之一的连通块的大小之和；由于连通块的性质，图上直接相连的两连通块颜色必然不同，因此枚举每个连通块及颜色，\(dfs\) 即可

实现细节上，首先，连边时记得开 \(vis\) 数组记录相邻的连通块是否已经连过边了，不要重复连边；其次，可以在连边时同时记录每个连通块相邻的连通块有什么颜色 (即 \(dfs\) 时该连通块除自身颜色的第二个颜色都有什么选择)，方便 \(dfs\)；每次枚举连通块，直接把该连通块所有的颜色可能 \(dfs\) 完，以后再遇到该连通块直接 \(continue\) 即可

代码

C++
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 505, MAXL = 7e4+5;

int N, cnt, recentsiz, ans1, ans2;
int mv[4][2] = {0, 1, 0, -1, 1, 0, -1, 0};
int mp[MAXN][MAXN], belong[MAXN][MAXN];
bool vis[MAXN][MAXN];

map <int, bool> visedge[MAXL];

struct Node{
    int siz;
    int col;
}node[MAXL];

vector <int> G[MAXL];

void dfs(int x, int y, int tp){
    belong[x][y] = cnt;
    node[cnt].siz++;

    for (int i=0; i<4; i++){
        int nx = x+mv[i][0];
        int ny = y+mv[i][1];

        if (nx<1 || ny<1 || nx>N || ny>N){
            continue;
        }
        if (mp[nx][ny] != tp || vis[nx][ny] == true){
            continue;
        }

        vis[nx][ny] = true;
        dfs(nx, ny, tp);
    }
}

vector <int> colors[MAXL];
map <int, bool> vis_2[MAXL];

void dfs_2(int nod, int col1, int col2){
    recentsiz += node[nod].siz;
    for (int i=0; i<G[nod].size(); i++){
        if (node[G[nod][i]].col == col1 && vis_2[G[nod][i]][col2] == false){
            vis_2[G[nod][i]][col2] = true;
            dfs_2(G[nod][i], col1, col2);       
        }
        else if (node[G[nod][i]].col == col2 && vis_2[G[nod][i]][col1] == false){
            vis_2[G[nod][i]][col1] = true;
            dfs_2(G[nod][i], col1, col2);   
        }
    }   
}

int main(){
    scanf("%d", &N);

    for (int i=1; i<=N; i++){
        for (int j=1; j<=N; j++){
            scanf("%d", &mp[i][j]);
        }
    }

    for (int i=1; i<=N; i++){
        for (int j=1; j<=N; j++){
            if (vis[i][j] == false){
                cnt++;
                node[cnt].col = mp[i][j];
                vis[i][j] = true;
                dfs(i, j, mp[i][j]);
            }   
        }
    }

    for (int i=1; i<=cnt; i++){
        ans1 = max(ans1, node[i].siz);
    }

    int i, j, k;
    for (i=1; i<=N; i++){
        for (j=1; j<=N; j++){
            for (k=0; k<4; k++){
                int nx = i+mv[k][0];
                int ny = j+mv[k][1];

                if (nx<1 || ny<1 || nx>N || ny>N){
                    continue;
                }
                if (visedge[belong[nx][ny]][belong[i][j]] == false){
                    visedge[belong[nx][ny]][belong[i][j]] = true;
                    visedge[belong[i][j]][belong[nx][ny]] = true;               

                    G[belong[nx][ny]].push_back(belong[i][j]);
                    G[belong[i][j]].push_back(belong[nx][ny]);
                    colors[belong[nx][ny]].push_back(node[belong[i][j]].col);
                    colors[belong[i][j]].push_back(node[belong[nx][ny]].col);
                }
            }
        }
    }

    for (int i=1; i<=cnt; i++){
        for (int j=0; j<colors[i].size(); j++){
            if (vis_2[i][colors[i][j]] == false){
                vis_2[i][colors[i][j]] = true;
                recentsiz = 0;
                dfs_2(i, node[i].col, colors[i][j]);
                ans2 = max(ans2, recentsiz);
            }   
        }
    }

    printf("%d\n%d", ans1, ans2);
    return 0;
}

评论