2024.7.17 训练记录
BNDSOJ USACO - Connect The Cows
Connect The Cows
一开始拿到这道题,脑残直接开始一格一格 \(dfs\),难想、复杂又容易写错……实际上,由于约翰 只会在牛处转向,我们只需要在原点 \((0, 0)\) 和牛之间 \(dfs\) 即可
我们枚举每只牛的坐标,如果有两只牛 \(x\) 坐标相同或 \(y\) 坐标相同就在它们之间连边;注意,如果牛的 \(x\) 坐标为 \(0\) 或 \(y\) 坐标也为 \(0\),也别忘了在它与原点之间连边
\(dfs\) 时,我们记录当前节点编号、方向 与经过的牛的数量;别忘了记录方向!枚举与当前点直接连边的点,特判下个点是 \(0\) 且已经经过所有牛 的情况 (因为如果没有经过所有牛回到原点是没有意义的,反正也无法改变方向);若下个点为牛,必须转向,无需考虑不改变方向的情况 (假设从起始牛的位置向下走到中间牛,如果中间牛处不改变方向,只有在该头牛下方还有一头牛时有意义;又由于我们的连边操作,起始牛一定会向这一头牛连一条边,因此如果我们考虑不改变方向的情况,答案会被重复计算
代码
| C++ |
|---|
| #include<bits/stdc++.h>
using namespace std;
const int MAXN = 15;
int N, ans;
struct Cow{
int x;
int y;
}cow[MAXN];
struct Edge{
int to;
int dir;
};
vector <Edge> G[MAXN];
void show(){
cout << "show: " << endl;
for (int i=0; i<=N; i++){
for (int j=0; j<G[i].size(); j++){
cout << i << " " << G[i][j].to << ", dir = " << G[i][j].dir << endl;
}
}
}
bool vis[MAXN];
void dfs(int node, int dir, int cnt){
if (node == 0 && cnt == N+1){
ans++;
return;
}
for (int i=0; i<G[node].size(); i++){
if (dir == G[node][i].dir){
if (G[node][i].to == 0 && cnt == N+1){
dfs(G[node][i].to, dir, cnt);
}
if (G[node][i].to != 0 && vis[G[node][i].to] == false){
vis[G[node][i].to] = true;
for (int j=0; j<4; j++){
if (j != dir){
dfs(G[node][i].to, j, cnt+1);
}
}
vis[G[node][i].to] = false;
}
}
}
}
int main(){
scanf("%d", &N);
for (int i=1; i<=N; i++){
scanf("%d%d", &cow[i].x, &cow[i].y);
if (cow[i].x == 0){
if (cow[i].y > 0){
G[0].push_back({i, 0});
G[i].push_back({0, 2});
}
else{
G[0].push_back({i, 2});
G[i].push_back({0, 0});
}
}
else if (cow[i].y == 0){
if (cow[i].x > 0){
G[0].push_back({i, 3});
G[i].push_back({0, 1});
}
else{
G[0].push_back({i, 1});
G[i].push_back({0, 3});
}
}
}
for (int i=1; i<=N; i++){
for (int j=i+1; j<=N; j++){
if (cow[i].x == cow[j].x){
if (cow[i].y > cow[j].y){
G[i].push_back({j, 2});
G[j].push_back({i, 0});
}
else{
G[i].push_back({j, 0});
G[j].push_back({i, 2});
}
}
else if (cow[i].y == cow[j].y){
if (cow[i].x > cow[j].x){
G[i].push_back({j, 1});
G[j].push_back({i, 3});
}
else{
G[i].push_back({j, 3});
G[j].push_back({i, 1});
}
}
}
}
// show();
vis[0] = true;
dfs(0, 0, 1);
dfs(0, 1, 1);
dfs(0, 2, 1);
dfs(0, 3, 1);
printf("%d", ans);
return 0;
}
|
BNDSOJ USACO - Wrong Directions
Wrong Directions
我们如果每次更改一个字符串,再从头扫一遍,时间复杂度为 \(O(n^2)\),显然会超时
我们优化暴力,考虑将原字符串分为三段,具体的,为更改的字符、更改的字符前段、更改的字符后段三段;我们考虑对长度为 \(N\) 的原字符串 \(s[i]\) 进行预处理,由于我们 只需要知道更改前段走到哪里、更改后段相较于原点的相对距离,因此预处理出 前缀位置数组 \(before[i]\),记录按照子串 \(s[1...i]\) 操作后走到的位置;再处理出 后缀位置数组 \(after[i]\),记录按照子串 \(s[i...N]\) 操作后走到的位置 (起始方向都默认向北);
我们发现,\(before[i]\) 数组是容易维护的,但由于 \(after[i]\) 数组是倒着处理的,不能按照常规方法维护;考虑分类讨论第 \(i\) 位的字符种类:
- 如果为 \(F\),那很好办,直接令 \(after[i].x = after[i+1].x\),\(after[i].y = after[i+1].y+1\) 即可,因为默认起始方向向北,向前走一步即为向北走一步,体现在 \(y\) 坐标的变化上
- 如果为 \(L\),那么原来的 \(y\) 移动量变成了现在的 \(x\) 移动量,原来的 \(x\) 移动量变成了现在的 \(y\) 移动量;至于方向,我们可以画个图辅助理解
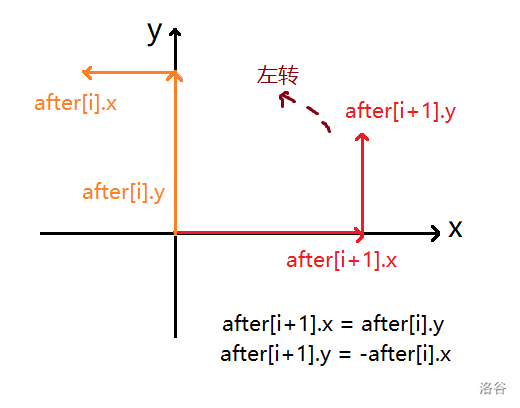
此时有 \(after[i].x = -after[i+1].y, after[i].y = after[i+1].x\)
- 如果为 \(R\),那么原来的 \(y\) 移动量还是变成了现在的 \(x\) 移动量,原来的 \(x\) 移动量也还是变成了现在的 \(y\) 移动量;其实图与左转时是相同的,只不过左转时的 \(after[i]\) 相当于右转时的 \(after[i+1]\)、左转时的 \(after[i+1]\) 相当于右转时的 \(after[i]\);类似的,此时有 \(after[i].x = after[i+1].y, after[i].y = -after[i+1].x\)
这样,我们就能够处理出 \(after[i]\) 数组了;实际更改第 \(i\) 位时,只需要先将位置变更为 \(before[i-1]\),讨论第 \(i\) 位的变化,再两坐标分别增加 \(after[i+1].x\)、\(after[i+1].y\) 即可;
实现时,注意我们在处理 \(after[i]\) 数组时默认方向向北,但更改字符时可能会改变方向,使方向不是北,因此我们需要考虑方向的变化;具体的,如果方向变成西 / 东,那相当于一次 左转 / 右转,否则相当于一次 按原点对称翻转
代码
| C++ |
|---|
| #include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;
string s;
int ans;
map <int, map<int, bool> > vis;
struct Node{
int x;
int y;
int dir;
}before[MAXN], after[MAXN];
pair<int, int> getnex(int x, int y, int dir){
int nx, ny;
if (dir == 0){
nx = x;
ny = y+1;
}
else if (dir == 1){
nx = x-1;
ny = y;
}
else if (dir == 2){
nx = x;
ny = y-1;
}
else{
nx = x+1;
ny = y;
}
return {nx, ny};
}
pair <int, int> offset(int x, int y, int dir){
if (dir == 1){
return {-y, x};
}
if (dir == 0){
return {x, y};
}
if (dir == 2){
return {-x, -y};
}
if (dir == 3){
return {y, -x};
}
}
int main(){
cin >> s;
before[0].x = 0;
before[0].y = 0;
before[0].dir = 0;
for (int i=1; i<=s.size(); i++){
if (s[i-1] == 'L'){
before[i] = before[i-1];
before[i].dir = (before[i].dir+1)%4;
}
else if (s[i-1] == 'R'){
before[i] = before[i-1];
before[i].dir = (before[i].dir+3)%4;
}
else{
int nx, ny;
nx = getnex(before[i-1].x, before[i-1].y, before[i-1].dir).first;
ny = getnex(before[i-1].x, before[i-1].y, before[i-1].dir).second;
before[i] = {nx, ny, before[i-1].dir};
}
}
for (int i=s.size(); i>=1; i--){
if (s[i-1] == 'L'){
after[i].x = -after[i+1].y;
after[i].y = after[i+1].x;
}
else if (s[i-1] == 'R'){
after[i].x = after[i+1].y;
after[i].y = -after[i+1].x;
}
else{
after[i].x = after[i+1].x;
after[i].y = after[i+1].y+1;
}
}
for (int i=1; i<=s.size(); i++){
int ansx = before[i-1].x, ansy = before[i-1].y, ansdir = before[i-1].dir;
if (s[i-1] == 'F'){
int offsetx = offset(after[i+1].x, after[i+1].y, (ansdir+1)%4).first;
int offsety = offset(after[i+1].x, after[i+1].y, (ansdir+1)%4).second;
int nx = ansx+offsetx;
int ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
offsetx = offset(after[i+1].x, after[i+1].y, (ansdir+3)%4).first;
offsety = offset(after[i+1].x, after[i+1].y, (ansdir+3)%4).second;
nx = ansx+offsetx;
ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
}
else if (s[i-1] == 'L'){
int offsetx = offset(after[i+1].x, after[i+1].y, (ansdir+3)%4).first;
int offsety = offset(after[i+1].x, after[i+1].y, (ansdir+3)%4).second;
int nx = ansx+offsetx;
int ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
offsetx = offset(after[i+1].x, after[i+1].y+1, ansdir).first;
offsety = offset(after[i+1].x, after[i+1].y+1, ansdir).second;
nx = ansx+offsetx;
ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
}
else if (s[i-1] == 'R'){
int offsetx = offset(after[i+1].x, after[i+1].y, (ansdir+1)%4).first;
int offsety = offset(after[i+1].x, after[i+1].y, (ansdir+1)%4).second;
int nx = ansx+offsetx;
int ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
offsetx = offset(after[i+1].x, after[i+1].y+1, ansdir).first;
offsety = offset(after[i+1].x, after[i+1].y+1, ansdir).second;
nx = ansx+offsetx;
ny = ansy+offsety;
//cout << nx << " " << ny << endl;
if (!vis[nx][ny]){
vis[nx][ny] = true;
ans++;
}
}
}
printf("%d", ans);
return 0;
}
|
BNDSOJ USACO - Three Lines
Three Lines
看到题,想到一个看起来很对的贪心:我们按照每行有多少头牛从大到小排序、每列有多少头牛从大到小排序,删去牛最多的一行、牛最多的一列,再判断剩下的牛是否能够用一行或一列覆盖
我们感性理解一下这个贪心;如果我们用两行一列或两列一行删牛,一定会删一行或一列,那么对于删的这一行 / 一列,我们希望删完之后尽可能减小接下来再删列 / 行 的压力,因此我们删包含牛最多的一行 / 一列
这时候,你发现这样感性理解有一个很显然的漏洞:如果我们根本不用行或不用列,直接用三行 / 三列删牛怎么办?是的,贪心在这种情况下正确性无法保证,因此我们需要 特判使用三行或三列能否删掉所有牛
不特判的反例如下:
这样我们会删除第一行和第二列,剩余的牛无法用一行或一列覆盖;但实际上,我们直接用三行或者三列就可以删掉所有的牛
代码
| C++ |
|---|
| #include<bits/stdc++.h>
using namespace std;
const int MAXN = 5e4+5;
int N, row, col, trow, tcol;
struct Cow{
int x;
int y;
}cow[MAXN];
map <int, bool> vis1, vis2, t1, t2;
map <int, int> rc, cr, rc2, cr2;
int main(){
scanf("%d", &N);
for (int i=1; i<=N; i++){
scanf("%d%d", &cow[i].x, &cow[i].y);
if (vis1[cow[i].x] == false){
vis1[cow[i].x] = true;
row++;
}
if (vis2[cow[i].y] == false){
vis2[cow[i].y] = true;
col++;
}
}
if (row <= 3 || col <= 3){
printf("1");
return 0;
}
for (int i=1; i<=N; i++){
rc[cow[i].x]++;
cr[cow[i].y]++;
}
for (auto it = rc.begin(); it != rc.end(); it++){
rc2[(*it).second] = (*it).first;
}
for (auto it = cr.begin(); it != cr.end(); it++){
cr2[(*it).second] = (*it).first;
}
auto brc = rc2.end();
brc--;
auto bcr = cr2.end();
bcr--;
int mrc = (*brc).second;
int mcr = (*bcr).second;
// cout << mrc << " " << mcr;
for (int i=1; i<=N; i++){
if (cow[i].x == mrc || cow[i].y == mcr){
continue;
}
if (t1[cow[i].x] == false){
t1[cow[i].x] = true;
trow++;
}
if (t2[cow[i].y] == false){
t2[cow[i].y] = true;
tcol++;
}
}
if (trow == 1 || tcol == 1){
printf("1");
return 0;
}
printf("0");
return 0;
}
|
BNDSOJ USACO - Islands
Islands
我们考虑暴力,如果暴力枚举水的高度,然后扫一遍原序列统计岛屿的个数,时间复杂度为 \(O(HN)\),\(H\) 是值域,这里为 \(1e9\),显然会爆炸
我们发现值域实在是太大了,怎样避免枚举每个值呢?注意到,如果岛屿个数发生变化,临界点 必然是水的高度与之前某一还没有被淹没的陆机的高度相同时;又因为随着水位逐渐涨高,被淹没的陆地高度也会相应变高,因此我们 对陆地按照高度从小到大排序,依次处理淹没即可;这样时间复杂度变为 \(O(N^2)\),还是会超时
我们考虑优化如何统计岛屿个数。考虑水位上涨引起的岛屿个数的变化;具体的,设淹没前有 \(cnt\) 个岛屿,当前为第 \(i\) 块陆地被淹没,分情况讨论:
- 第 \(i-1\) 块与第 \(i+1\) 块陆地都被淹没,此时 \(cnt=cnt-1\)
- 第 \(i-1\) 块与第 \(i+1\) 块陆地有且仅有一块被淹没,此时 \(cnt\) 不变
- 第 \(i-1\) 块与第 \(i+1\) 块陆地都没有被淹没,此时 \(cnt=cnt+1\)
那么如果淹没的陆地的旁边是岸怎么办?没关系,初始时令第 \(0\) 块陆地 (左岸) 与第 \(N+1\) 块陆地 (右岸) 也被淹没,之后正常统计即可;这样维护每次更改的时间复杂度就为 \(O(1)\)
时间复杂度 \(O(NlogN)\)
| C++ |
|---|
| #include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;
int N, ans;
int h[MAXN];
bool deleted[MAXN];
struct Node{
int val;
int pos;
}sorth[MAXN];
bool cmp(Node a, Node b){
return a.val < b.val;
}
int main(){
scanf("%d", &N);
for (int i=1; i<=N; i++){
scanf("%d", &h[i]);
sorth[i].val = h[i];
sorth[i].pos = i;
}
sort(sorth+1, sorth+N+1, cmp);
deleted[0] = true;
deleted[N+1] = true;
int recenth = -1, cnt = 1;
for (int i=1; i<=N; ){
if (sorth[i].val != recenth){
ans = max(ans, cnt);
recenth = sorth[i].val;
}
else{
int delpos = sorth[i].pos;
deleted[delpos] = true;
if (deleted[delpos-1] && deleted[delpos+1]){
cnt--;
}
else if ((!deleted[delpos-1]) && (!deleted[delpos+1])){
cnt++;
}
i++;
}
}
ans = max(ans, cnt);
printf("%d", ans);
return 0;
}
|
P5120 USACO - Convention II S
P5120
考虑按照题意模拟,令 \(topend\) 为当前吃草的牛吃完草的时间,\(cow[i].a\) 为第 \(i\) 头牛到达的时间,\(cow[i].t\) 为第 \(i\) 头牛吃草的时间;由于每次来的牛,按照资历 (即输入先后顺序) 排序,因此我们 定义一个优先队列,也按照输入先后顺序排序,模拟排队
当第 \(i\) 头牛到达时,我们分情况讨论如下:
-
草地上有牛在吃,那么让第 \(i\) 头牛直接入队等待
-
草地上没有牛在吃
2.1 队列中没有牛等待,直接让第 \(i\) 头牛吃即可;注意,不是入队,此时直接令 \(topend = cow[i].a+cow[i].t\)
2.2 队列中有牛等待,那么 让队首的牛去吃草
,同时 统计队首的牛的等待时间 (注意不是立马统计第 \(i\) 头牛的等待时间),队首的牛在 \(q.top().a\) 时前来,在 \(topend\) 时吃上草,因此其等待时间为 \(topend-q.top().a\);别忘了在统计后更新 \(topend\),加上 \(q.top().t\),因为当前队首牛也得吃一会;注意,如果当前队首牛吃完的时间 (也就是更新后的 \(topend\)) 仍然小于 \(cow[i].a\),那么我们 重新处理第 \(i\) 头牛的情况,因为可能会需要更改出队信息,即队列中一些看起来在排队的牛实际上已经吃完了;当然,如果更新后的 \(topend\) 大于等于 \(cow[i].a\),那么说明还得等,直接让第 \(i\) 头牛入队即可
注意,处理完所有牛的到达操作后,可能队列里还有牛,因为会有没吃完的情况;此时按一样的方法维护队列,依次让队首牛出队,直到队列里没有牛即可
代码
| C++ |
|---|
| #include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+5;
int N, ans;
struct Cow{
int a;
int t;
int id;
bool operator > (const Cow c) const {
return c.id < id;
}
}cow[MAXN];
priority_queue <Cow, vector<Cow>, greater<Cow> > q;
bool cmp(Cow a, Cow b){
return a.a < b.a;
}
int main(){
scanf("%d", &N);
for (int i=1; i<=N; i++){
scanf("%d%d", &cow[i].a, &cow[i].t);
cow[i].id = i;
}
sort(cow+1, cow+N+1, cmp);
// cout << cow[1].id << endl;
int topend = cow[1].a+cow[1].t;
for (int i=2; i<=N; i++){
if (topend <= cow[i].a){
if (q.empty()){
topend = cow[i].a+cow[i].t;
}
else{
ans = max(ans, topend-q.top().a);
topend += q.top().t;
q.pop();
if (topend < cow[i].a){
i--;
}
else{
q.push(cow[i]);
}
}
}
else{
q.push(cow[i]);
}
}
while (!q.empty()){
ans = max(ans, topend-q.top().a);
topend += q.top().t;
q.pop();
}
printf("%d", ans);
return 0;
}
|
